前言
最近在梳理算法知识体系时,遇到了
myAtoi这道经典的字符串转整数问题。官方题解给出了自动机的解法。坦白说,我对这个概念感到相当生疏,所以在这对自动机做个笔记。
题目描述

自动机解题
思路
字符串处理的题目往往涉及复杂的流程以及条件情况,如果直接上手写程序,一不小心就会写出极其臃肿的代码。
因此,为了有条理地分析每个输入字符的处理方法,我们可以使用自动机这个概念:
我们的程序在每个时刻有一个状态 s,每次从序列中输入一个字符 c,并根据字符 c 转移到下一个状态 s'。这样,我们只需要建立一个覆盖所有情况的从 s 与 c 映射到 s' 的表格即可解决题目中的问题。
算法图示
本题可以建立如下图所示的自动机:
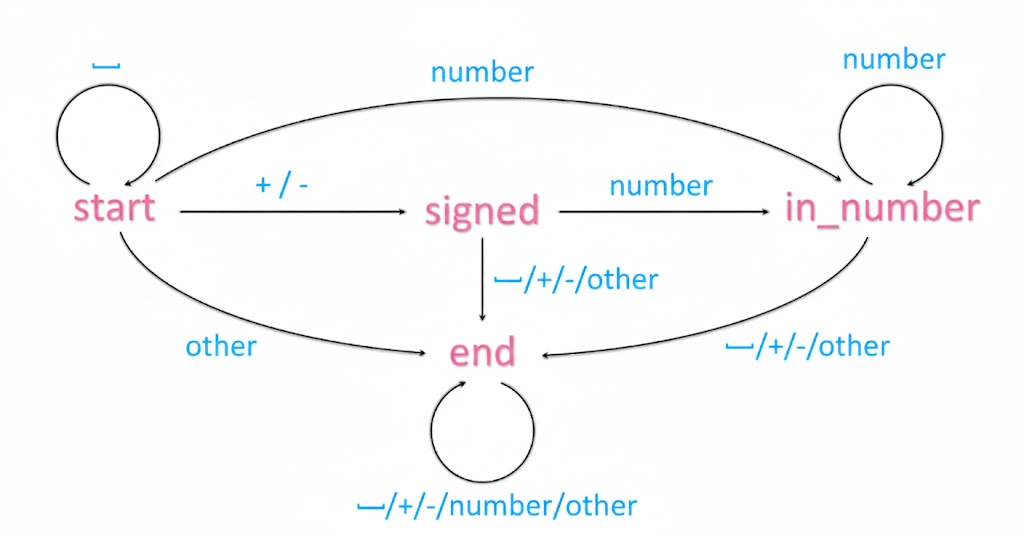
转成状态转移表格如下:
| 当前状态 (Current State) | 输入 (' ') | 输入 ('+/-') | 输入 (number) | 输入 (other) |
|---|---|---|---|---|
| start | start | signed | in_number | end |
| signed | end | end | in_number | end |
| in_number | end | end | in_number | end |
| end | end | end | end | end |
于是我们只需将这个表格用代码表达出来。
代码实现
1. 定义状态 (State) 和输入类型 (CharType)
// 定义解析过程中可能遇到的所有状态
enum State {
START, // 初始状态
SIGNED, // 遇到符号之后的状态
IN_NUMBER, // 正在读取数字的状态
END // 终止状态
}
// 将输入字符归纳为几种类型
enum CharType {
SPACE,
SIGN,
DIGIT,
OTHER
}
2. Automaton 主类
这个类将封装状态机的所有逻辑:当前状态、符号、数值,以及最核心的状态转移表。这种表驱动法(Table-Driven Method)是状态机模式的精髓。
import java.util.HashMap;
import java.util.Map;
// 主解决方案类,负责调用自动机
class Solution {
public int myAtoi(String s) {
Automaton automaton = new Automaton();
for (int i = 0; i < s.length(); i++) {
automaton.process(s.charAt(i));
}
// 最终结果由自动机内部的符号和数值计算得出
return (int) (automaton.sign * automaton.ans);
}
}
// 自动机核心实现类
class Automaton {
// 成员变量:符号、数值(用 long 防溢出)、当前状态
public int sign = 1;
public long ans = 0;
private State currentState = State.START;
// 核心:状态转移表 Map<当前状态, Map<输入类型, 下一状态>>
private final Map<State, Map<CharType, State>> table;
public Automaton() {
// 在构造函数中初始化状态转移表,定义所有规则
table = new HashMap<>();
// 定义 START 状态下,遇到四种输入类型分别转移到哪个状态
Map<CharType, State> startMap = new HashMap<>() {{
put(CharType.SPACE, State.START);
put(CharType.SIGN, State.SIGNED);
put(CharType.DIGIT, State.IN_NUMBER);
put(CharType.OTHER, State.END);
}};
table.put(State.START, startMap);
// 定义 SIGNED 状态下的转移规则
Map<CharType, State> signedMap = new HashMap<>() {{
put(CharType.SPACE, State.END);
put(CharType.SIGN, State.END);
put(CharType.DIGIT, State.IN_NUMBER);
put(CharType.OTHER, State.END);
}};
table.put(State.SIGNED, signedMap);
// 定义 IN_NUMBER 状态下的转移规则
Map<CharType, State> inNumberMap = new HashMap<>() {{
put(CharType.SPACE, State.END);
put(CharType.SIGN, State.END);
put(CharType.DIGIT, State.IN_NUMBER);
put(CharType.OTHER, State.END);
}};
table.put(State.IN_NUMBER, inNumberMap);
// 定义 END 状态下的转移规则(所有输入都停在 END)
Map<CharType, State> endMap = new HashMap<>() {{
put(CharType.SPACE, State.END);
put(CharType.SIGN, State.END);
put(CharType.DIGIT, State.END);
put(CharType.OTHER, State.END);
}};
table.put(State.END, endMap);
}
// 辅助方法,将具体字符映射为输入类型
private CharType getCharType(char c) {
if (Character.isWhitespace(c)) return CharType.SPACE;
if (c == '+' || c == '-') return CharType.SIGN;
if (Character.isDigit(c)) return CharType.DIGIT;
return CharType.OTHER;
}
// 核心处理逻辑:接收一个字符,驱动状态机运转
public void process(char c) {
if (currentState == State.END) {
return; // 已经进入终止状态,不再处理任何字符
}
CharType type = getCharType(c);
// **关键**:在状态转移之前,根据【当前状态】和【输入】执行相应的动作
// 这是状态机与业务逻辑(计算数值、判断符号、检查溢出)结合的地方
if (currentState == State.IN_NUMBER && type == CharType.DIGIT) {
int digit = c - '0';
// 溢出检查:在 ans * 10 + digit > MAX_VALUE 之前进行判断
if (ans > (Integer.MAX_VALUE - digit) / 10) {
// 根据符号决定溢出后的值
ans = (sign == 1) ? Integer.MAX_VALUE : (long)Integer.MAX_VALUE + 1;
sign = 1; // 符号已经融入 ans,重置 sign
currentState = State.END; // 提前终止
return;
}
ans = ans * 10 + digit;
} else if (currentState == State.START) {
if (type == CharType.SIGN) {
sign = (c == '+') ? 1 : -1;
} else if (type == CharType.DIGIT) {
ans = ans * 10 + (c - '0');
}
} else if (currentState == State.SIGNED && type == CharType.DIGIT) {
ans = ans * 10 + (c - '0');
}
// **状态转移**:根据表格更新到下一个状态
currentState = table.get(currentState).get(type);
}
}
这份代码清晰地将**状态转移逻辑(table)与业务动作(if/else块)和驱动流程(process方法)**分离开来,是状态机模式的经典实现。
扩展介绍:有限自动机 (Finite Automaton)
myAtoi 只是冰山一角。有限自动机(FA)或称有限状态机(FSM),是计算机科学的理论基石之一,也是解决海量工程问题的实用设计模式。
1. 什么是有限自动机?(The Formal Stuff)
有限状态自动机(Finite State Machine, FSM)是一种抽象计算模型,形式化定义为一个五元组 $$ (Q, \Sigma,\delta, q_0, F) $$ 其中:
$$ Q $$
:为一个有限的状态集合 (A finite set of states)。在
myAtoi中,就是{START, SIGNED, IN_NUMBER, END}。$$ \Sigma $$
:一个有限的输入符号(或字母表)集合 (A finite set of input symbols)。在
myAtoi中,我们将其抽象为{SPACE, SIGN, DIGIT, OTHER}。$$ \delta $$
:转移函数 (The transition function)。它定义了状态如何根据输入进行改变。其形式为: $$ \delta: Q \times \Sigma \rightarrow Q $$ 在
myAtoi中,我们的table就是这个转移函数的具体实现。例如,δ(START, SIGN) = SIGNED。$$ q_0 \in Q $$
:初始状态 (The start state),它是Q中一个元素。在
myAtoi中,就是START。$$ F \subseteq Q $$
:接受状态的集合 (A set of accept states),是Q的一个子集。如果输入字符串处理完毕后,自动机停在F中的某个状态,则该字符串被“接受”。在
myAtoi中,IN_NUMBER可被视为一个接受状态。
2.自动机的两大类型:DFA 与 NFA
myAtoi 题解使用的自动机是一种确定性有限自动机 (DFA),因为它的每一步行动都是唯一确定的。但还有一种更灵活的类型叫 NFA。
- 确定性有限自动机 (DFA - Deterministic Finite Automaton)
- 定义:对于任何一个状态和任何一个输入符号,转移函数最多只能指向一个下一状态。
- 特点:无歧义、执行引擎简单、匹配高效,时间复杂度严格为O(n)。
- 例子:我们的
myAtoi实现、grep等文本搜索工具、编译器中的词法分析器。
- 非确定性有限自动机 (NFA - Nondeterministic Finite Automaton)
- 定义:对于任何一个状态和任何一个输入符号,转移函数可以指向一个状态的集合(可以是零个、一个或多个)。甚至允许在不消耗任何输入的情况下改变状态(ε-转移)。
- 特点:构造灵活,能轻松地从正则表达式生成,支持回溯等复杂功能。
- 例子:大多数现代编程语言(Java, Python, JS)的正则引擎都基于 NFA,因为它能支持捕获组等高级功能,但代价是匹配速度在最坏情况下可能很慢。
任何 NFA 都可以被转换成一个等价的 DFA。这正是连接灵活设计(NFA)和高效执行(DFA)的桥梁。
3.共生关系:自动机与正则表达式
正则表达式和有限自动机在计算理论上是等价的。它们是描述同一类“语言”(即“正则语言”)的两种不同方式。
- 正则表达式 (The "What"):它是一种面向用户的、描述性的 DSL。你用它来声明**“你想要匹配什么样的字符串模式”**。
- 有限自动机 (The "How"):它是底层的、计算性的模型。它提供了具体的一步步的算法来**“如何识别出符合该模式的字符串”**。
当我们执行一个正则表达式时,引擎内部经历了一个类似编译器的过程:
- 解析 (Parsing):Regex 字符串被解析成一棵抽象语法树 (AST)。
- 编译 (Compilation):AST 被编译成一个 NFA,因为 Regex 的结构可以非常直观地映射为 NFA。
- 执行 (Execution):引擎可以选择直接模拟 NFA(支持回溯,功能强大),或者将其转换为 DFA 再执行(无回溯,速度极快)。
所以,对正则表达式性能的优化,本质上是在引导正则引擎构建一个更高效、更少歧义的状态机。
使用场景
对于状态繁多、事件密集的复杂对象,采用有限状态机范式进行设计,能够提升代码的逻辑清晰度,实现对事件处理逻辑的优雅封装。除了本文的 myAtoi 和正则表达式,它还被广泛应用于:
- 编译器和解释器:词法分析器将源码字符串切分成
Token。 - 网络协议栈:TCP 协议的连接管理就是经典的状态机(
LISTEN,ESTABLISHED...)。 - UI 开发和游戏 AI:游戏角色的 AI(巡逻、攻击、逃跑)、UI 页面的导航逻辑。




评论区