译者声明

本文翻译自 CSS-Tricks 网站的优秀文章：The “Most Hated” CSS Feature: cos() and sin()，原作者为 Juan Diego Rodríguez。

翻译此文旨在技术分享与学习交流。文中观点归原作者所有。由于译者水平有限，如有疏漏之处，欢迎指正。强烈推荐阅读原文以获取最准确的信息。

CSS “最令人讨厌”的特性：cos() 和 sin()

作者：Juan Diego Rodríguez

日期：2025年9月15日

真的有“最差”的 CSS 特性吗？当然没有，对吧？毕竟，这都取决于个人观点和经验。但如果我们非要达成共识，那么查阅 State of CSS 2025 的调查结果会是一个不错的起点。我正是这么做的，直接跳到“奖项”部分，然后我找到了它：那个任何 CSS 特性都不该背负的头衔——“最令人讨厌的特性”……

most_hated_feature

说实话，这让我很震惊。三角函数真的那么被人讨厌吗？我知道“讨厌”和“最差”不是一回事，但这个词听起来还是很难受。我也知道我有点小题大做了，毕竟“只有9.1%的受访者真正讨厌三角函数”。但在我看来，这已经是对它相当大的偏见了。

我想消除这 9.1% 的偏见。所以，在这个系列中，我希望能探讨一些 CSS 三角函数的实际用途。我们会将它们拆分成几个部分来学习，因为内容很多，而我发现把知识分成专注、易于消化的块状来学习是最容易掌握和记忆的。我们将从这个“最差”特性中最受欢迎的函数开始：sin() 和 cos()。

CSS 三角函数：“最令人讨厌”的 CSS 特性

sin() 和 cos()（您正在阅读本文！）
攻克 CSS tan() 函数（即将推出）
反三角函数：asin(), acos(), atan() 和 atan2()（即将推出）

`cos()` 和 `sin()` 到底是什么？

本节是为那些对 cos() 和 sin() 还不甚了解，或者只是想复习一下的朋友们准备的。如果你在高中三角函数测验中拿过高分，随时可以跳到下一节！

我觉得 cos() 和 sin() 有趣的地方在于——同时也是我认为人们对它们感到困惑的原因——我们可以用很多种方式来描述它们。我们不用费力去查。只要快速浏览一下维基百科页面，你就会看到数量惊人的、带有细微差别的定义。

我认为有些定义过于笼统，缺乏关于 sin() 和 cos() 这类三角函数本质功能的细节。相反，另一些定义又过于复杂和学术化，如果没有高级学位很难理解。

让我们选择一个折中的方式：单位圆。

来认识一下单位圆。它是一个半径为一个单位的圆：

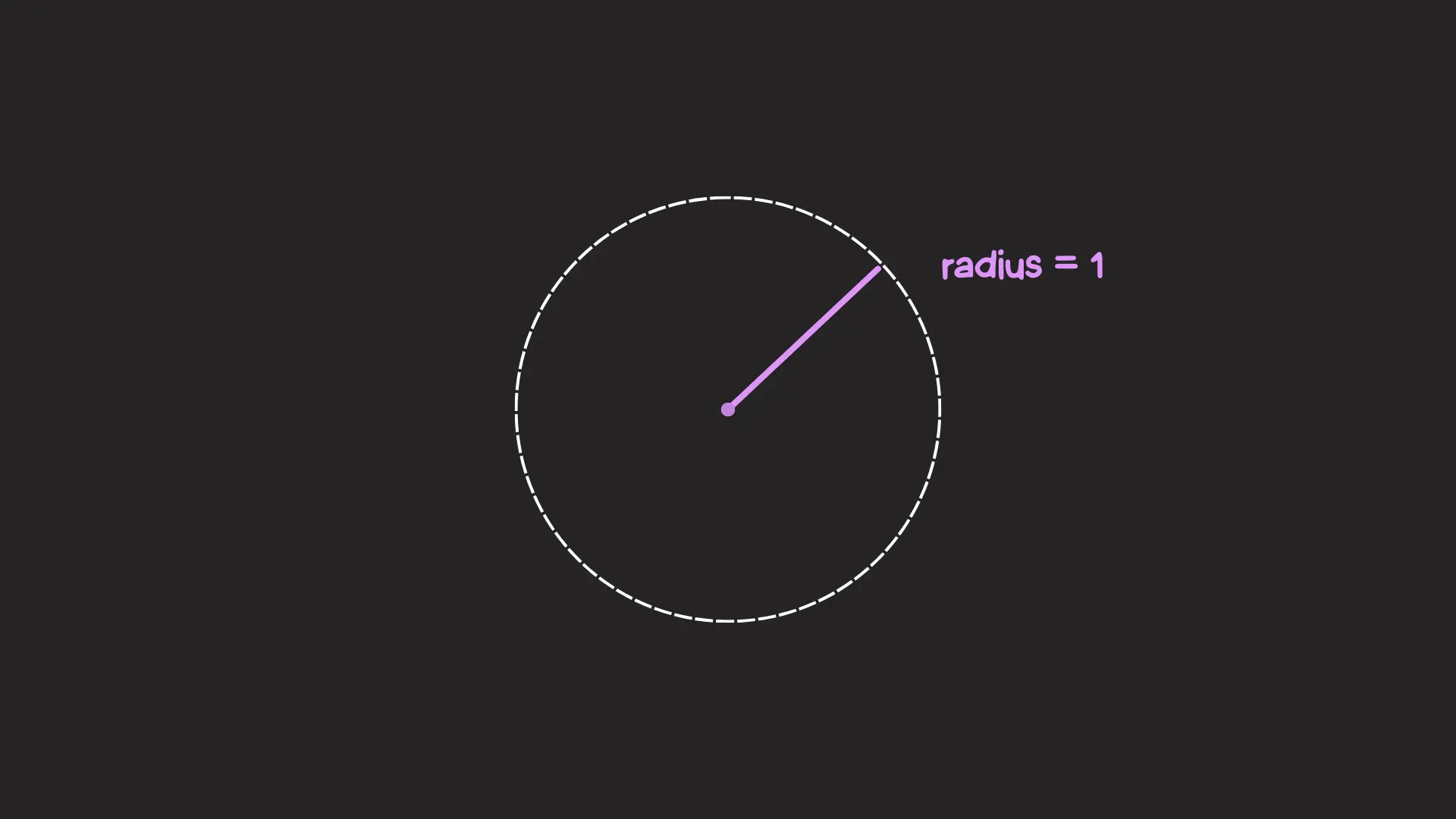
unit_circle_mdwuda

现在它独自……在坐空间当中。让我们把它放在笛卡尔坐标系（就是经典的带 X 和 Y 轴的图表）上。在笛卡尔坐标系中，我们这样描述空间中的每一个点：

X 坐标：水平轴，标示点向左或向右的位置。
Y 坐标：垂直轴，标示点向上或向下的位置。

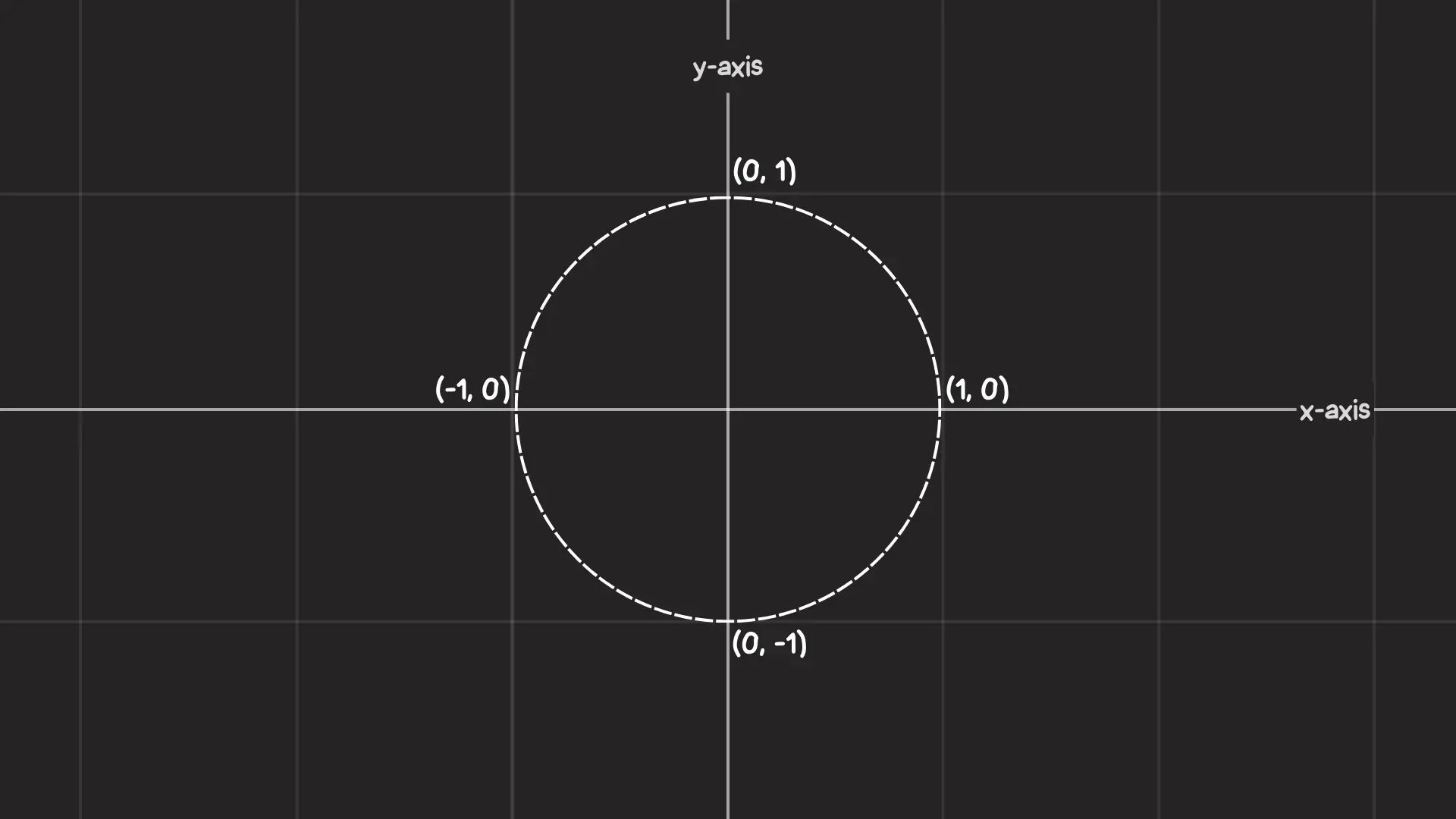
unit_circle_grid_fgfexz

我们可以通过一个角度在单位圆上移动，这个角度是从 X 轴正方向逆时针测量的。

See the Pen Unit circle - Example I by Juan Diego - Monknow (@monknow) on CodePen.

我们也可以使用负角度来顺时针移动。就像我的物理老师常说的：“时间是负的！”

注意，每个角度都对应单位圆上的一个唯一点。我们还能如何用笛卡尔坐标来描述那个点呢？

当角度为 0° 时，X 和 Y 坐标分别是 1 和 0 (1, 0)。我们也能轻松推断出其他角度的笛卡尔坐标，比如 90°、180° 和 270°。但对于任何其他角度，我们最初并不知道这个点在单位圆上的确切位置。

要是有一对函数，能接收一个角度并给出我们想要的坐标就好了……

你猜对了，CSS 的 cos() 和 sin() 函数正是做这个的。 它们关系非常密切，其中 cos() 用于处理 X 坐标，而 sin() 返回 Y 坐标。

在下面的演示中，可以拖动滑块看看这两个函数之间的关系，并注意它们如何与单位圆上的初始点形成一个直角三角形：

See the Pen Unit circle - Example II by Juan Diego - Monknow (@monknow) on CodePen.

我认为，目前你只需要了解这些关于 cos() 和 sin() 的知识就够了。它们映射到笛卡尔坐标，这使我们能通过一个角度追踪一个点在单位圆上的位置，无论这个圆有多大。

现在让我们深入探讨一下，在日常的 CSS 工作中，我们究竟能用 cos() 和 sin() 做些什么。将理论概念（如数学）与一些真实世界的场景联系起来总是好的。

环形布局

如果我们根据 cos() 和 sin() 的单位圆定义，就很容易理解它们如何被用来在 CSS 中创建环形布局。初始设置是一排圆形的元素：

See the Pen A normal arrangement of circles by Juan Diego - Monknow (@monknow) on CodePen.

假设我们想把每个圆形元素放置在一个更大圆形的轮廓上。首先，我们需要让 CSS 知道元素的总数以及每个元素的索引（它所在的顺序），我们可以通过一个内联 CSS 变量来实现：

<ul style="--total: 9">
  <li style="--i: 0">0</li>
  <li style="--i: 1">1</li>
  <li style="--i: 2">2</li>
  <li style="--i: 3">3</li>
  <li style="--i: 4">4</li>
  <li style="--i: 5">5</li>
  <li style="--i: 6">6</li>
  <li style="--i: 7">7</li>
  <li style="--i: 8">8</li>
</ul>

注意： 当 sibling-index() 和 sibling-count() 函数获得支持后，这一步会变得_非常_简单和简洁。在此期间，我使用内联 CSS 变量来硬编码索引。

为了将这些项目环绕在一个大圆的轮廓上，我们必须让它们按一定角度均匀分布。为了得到这个角度，我们可以用 360deg（一个完整的圆周）除以项目的总数。然后，要得到每个元素的具体角度，我们可以用这个角度间距乘以元素的索引（即位置）：

li {
  --rotation: calc(360deg / var(--total) * var(--i));
}

我们还需要将这些项目从中心推开，所以我们用另一个变量来指定圆的 --radius（半径）值。

ul {
  --radius: 10rem;
}

我们有了元素的角度和半径。剩下要做的就是计算每个项目的 X 和 Y 坐标。

这就是 cos() 和 sin() 发挥作用的地方。 我们用它们来获取每个项目在单位圆上的 X 和 Y 坐标，然后将每个坐标乘以 --radius 值，从而得到项目在大圆上的最终位置：

li {
  /* ... */
  position: absolute;
  transform: translateX(calc(cos(var(--rotation)) * var(--radius)))
             translateY(calc(sin(var(--rotation)) * var(--radius)));
}

就这样！我们得到了一系列均匀分布在一个大圆轮廓上的圆形项目：

See the Pen A circular arrangement of circles by Juan Diego - Monknow (@monknow) on CodePen.

而且我们并不需要使用一大堆“魔法数字”来实现它！我们只需要提供给 CSS 单位圆的半径，然后 CSS 就会完成所有那些让我们许多人称之为“最差”CSS 特性的三角函数运算。希望我已经说服你，如果你之前对它们有所抵触，现在能对它们有所改观！

我们不局限于完整的圆形！我们也可以通过选择 180deg 而不是 360deg 来实现半圆形排列。

See the Pen A circular arrangement of circles by Juan Diego - Monknow (@monknow) on CodePen.

这为布局开启了许多可能性。比如，如果我们想要一个从中心点展开的环形菜单，通过过渡圆的半径来实现？我们完全可以做到：

See the Pen Circular Layout by Juan Diego - Monknow (@monknow) on CodePen.

点击或悬停在标题上，菜单项就会围绕它形成一个圆形！

波浪形布局

在布局方面，我们还可以做更多的事情！比如说，如果我们在一个双轴图上绘制 cos() 和 sin() 的坐标，会注意到它们形成了一对周期性上下起伏的波浪。而且你会发现它们在水平（X）轴上是相互错开的：

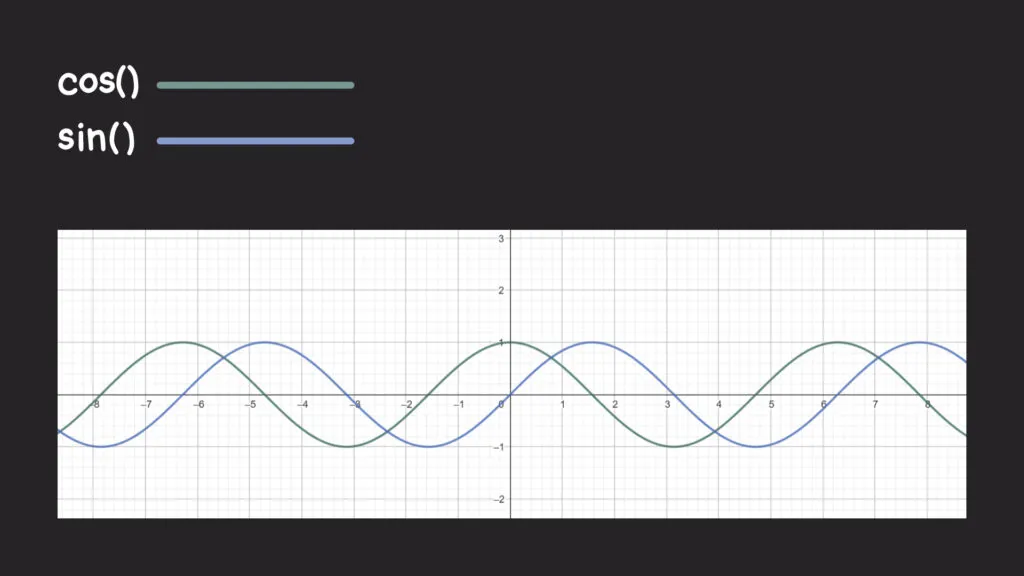
sine_cosine_waves-1024x576

这些波浪是从哪里来的？如果我们回想一下之前讨论的单位圆，cos() 和 sin() 的值在 -1 和 1 之间振荡。换句话说，当单位圆上的角度变化时，这些长度也随之匹配。如果我们将这种振荡绘制成图，我们就会得到波浪，并看到它们有点像彼此的镜像。

⚠️ 自动播放媒体

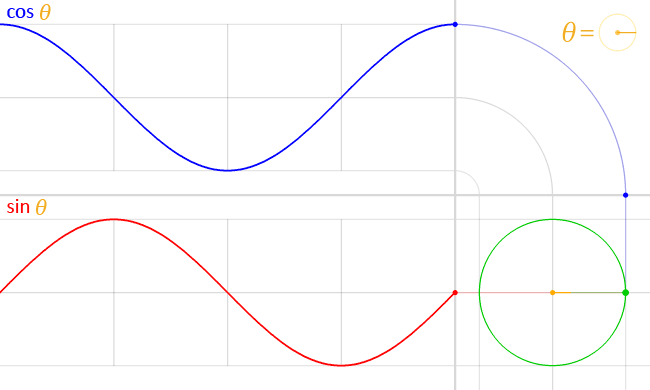
circle_cos_sin_k5uu75

我们能让一个元素沿着这些波浪之一进行布局吗？当然可以。让我们从之前创建的同样的一排圆形项目开始。但这一次，这一排的长度超出了视口，导致了溢出。

See the Pen Another normal arrangement of circles by Juan Diego - Monknow (@monknow) on CodePen.

我们会像之前一样为每个项目分配一个索引位置，但这次我们不需要知道项目的总数。

<ul>
  <li style="--i: 0"></li>
  <li style="--i: 1"></li>
  <li style="--i: 2"></li>
  <li style="--i: 3"></li>
  <li style="--i: 4"></li>
  <li style="--i: 5"></li>
  <li style="--i: 6"></li>
  <li style="--i: 7"></li>
  <li style="--i: 8"></li>
  <li style="--i: 9"></li>
  <li style="--i: 10"></li>
</ul>

我们希望沿着 sin() 或 cos() 波浪改变元素的垂直位置，这意味着根据每个项目在索引中的顺序来平移它的位置。我们将项目的索引乘以一个特定的角度，然后传递给 sin() 函数，它会返回一个比例，描述了元素在波浪上应该有多高或多低。最后一步是将这个结果乘以一个长度值，我计算的是项目总尺寸的一半。

用 CSS 的术语来表达这个数学运算就是：

li {
  transform: translateY(calc(sin(60deg * var(--i)) * var(--shape-size) / 2));
}

我用了 60deg 这个值，因为它产生的波浪比其他一些值更平滑，但我们可以随心所欲地改变它来获得更酷的波浪。在下一个演示中摆弄一下滑块，观察波浪的强度如何随角度变化：

See the Pen A wavy arrangement of circles by Juan Diego - Monknow (@monknow) on CodePen.

这是一个很好的例子，让我们看到了我们正在使用的东西，但你会在你的工作中如何使用它呢？想象一下，我们有两条这样波浪状的圆链，我们想让它们交织在一起，有点像 DNA 链。

假设我们从两个无序列表嵌套在另一个无序列表中的 HTML 结构开始。这两个嵌套的无序列表代表了形成链状图案的两条波浪：

<ul class="waves">
  <li>
    <ul class="principal">
      <li style="--i: 0"></li>
      <li style="--i: 1"></li>
      </ul>
  </li>
  <li>
    <ul class="secondary">
      <li style="--i: 0"></li>
      <li style="--i: 1"></li>
      </ul>
  </li>
</ul>

为了避免任何问题，我们将使用 display: contents 来忽略外部无序列表中包含其他列表的两个直接 <li> 元素。

.waves > li { display: contents; }

注意其中一条链是“principal”（主要的），而另一条是“secondary”（次要的）。区别在于“secondary”链被定位在“principal”链的后面。

See the Pen Yet another (longer) common arrangement of circles in a line by Juan Diego - Monknow (@monknow) on CodePen.

我们可以使用堆叠上下文（stacking context）来重新排序这些链：

.principal {
  position: relative;
  z-index: 2;
}
.secondary { 
  position: absolute; 
}

这将一条链放在另一条的上面。接下来，我们将使用“被讨厌的” sin() 和 cos() 函数来调整每个项目的垂直位置。记住，它们有点像彼此的镜像，所以两者之间的差异正是使波浪偏移形成两条相交链的原因：

.principal li {
  transform: translateY(calc(sin(60deg * var(--i)) * var(--shape-size) / 2));
}
.secondary li {
  transform: translateY(calc(cos(60deg * var(--i)) * var(--shape-size) / 2));
}

我们可以通过将 .secondary 波浪再移动 60deg 来进一步强调偏移：

.secondary li {
  transform: translateY(calc(cos(60deg * var(--i) + 60deg) * var(--shape-size) / 2));
}

下一个演示展示了波浪如何以 60deg 的偏移角度相交。调整滑块，看看波浪在不同角度下如何相交：

See the Pen Wavy Layout by Juan Diego - Monknow (@monknow) on CodePen.

哦，我告诉过你这可以用在实际的、真实世界的场景中。如何为一个英雄横幅（hero banner）增添一点奇思妙想和风采呢：

See the Pen Better Wavy Layout by Juan Diego - Monknow (@monknow) on CodePen.

阻尼振荡动画

最后一个例子让我思考：有没有办法利用 sin() 和 cos() 的来回运动来制作动画？ 我首先想到的例子是一个同样来回运动的动画，比如钟摆或弹跳的球。

当然，这很简单，因为我们可以在一个 animation 声明中完成：

.element {
  animation: someAnimation 1s infinite alternate;
}

这种“来回”的动画被称为_振荡_运动。虽然 cos() 或 sin() 可以用来模拟 CSS 中的振荡，但这就像重新发明轮子（而且还是一个更笨重的轮子）。

我了解到，完美的振荡运动——比如一个永不停歇的钟摆，或者一个永远不会停止弹跳的球——实际上并不存在。运动会随着时间推移而衰减，就像一个弹跳的弹簧：

damped_spring_nwegdi

⚠️ 自动播放媒体

有一个专门的术语来描述这个现象：_阻尼_振荡运动。你猜怎么着？我们可以用 cos() 函数在 CSS 中模拟它！如果我们将它随时间的变化绘制成图，我们会看到它来回运动，同时越来越接近静止位置。

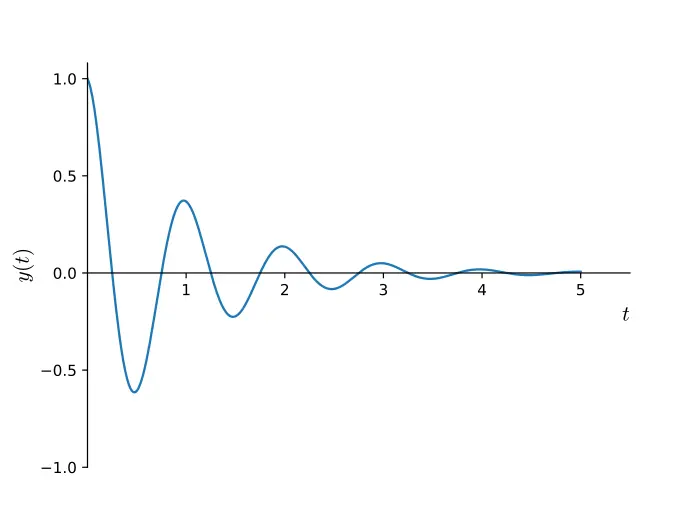
damped_movement_gfyswm

通常，我们可以将随时间变化的阻尼振荡描述为一个数学函数：

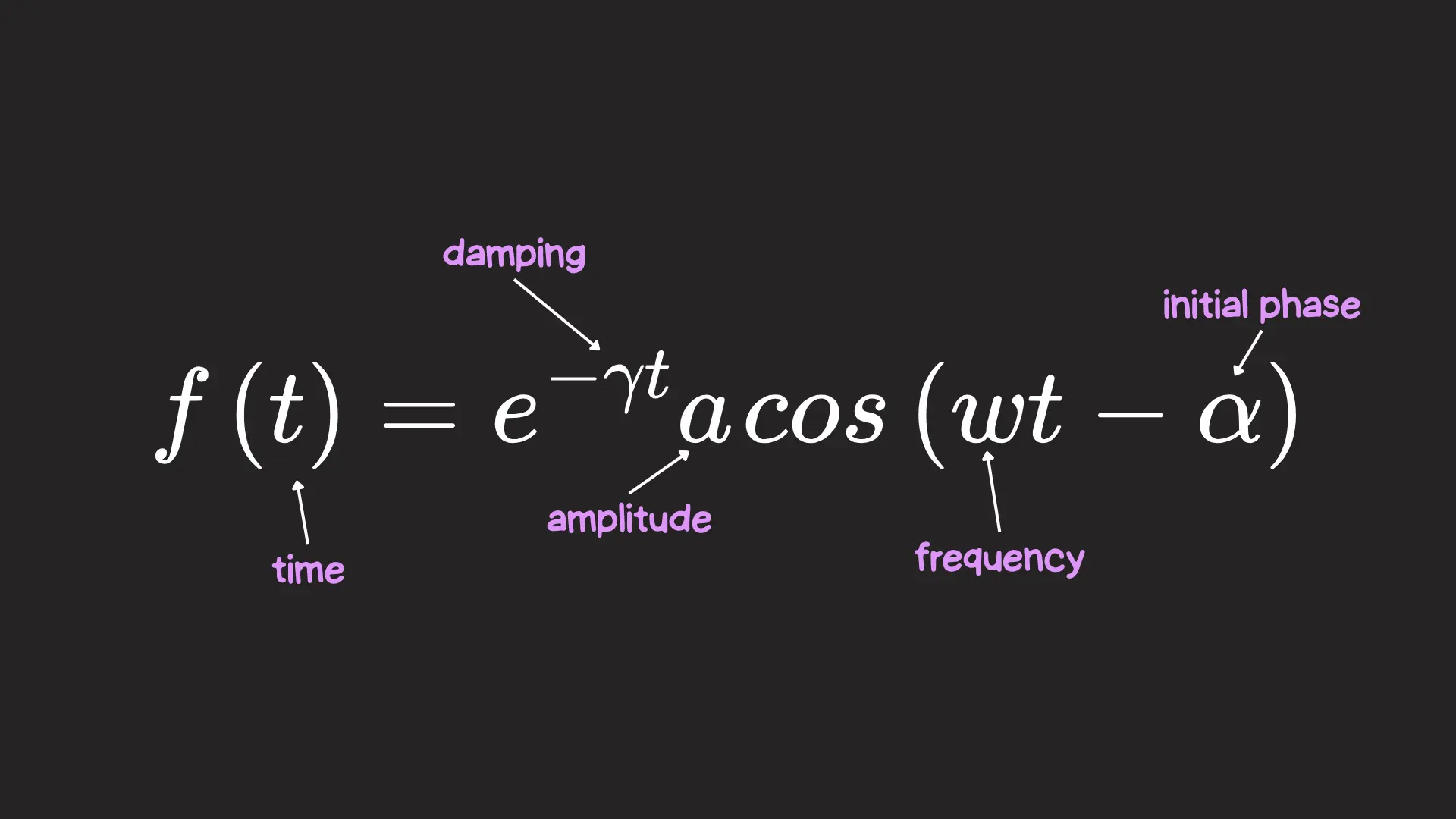
damped_oscillation_formula

它由三部分组成：

e-γt：由于负指数的存在，它会随着时间的推移呈指数级变小，使运动逐渐停止。它乘以一个阻尼常数 (γ)，该常数指定了运动衰减的速度。
a：这是振荡的初始振幅，即元素的初始位置。
cos(ωt−α)：这部分赋予了运动随时间变化的振荡特性。时间乘以频率 (ω)，它决定了元素的振荡速度。我们还可以从时间中减去 α，用来偏移系统的初始振荡。

好了，理论说够了！我们如何在 CSS 中实现它呢？我们将从一个单独的圆开始。

See the Pen A normal, common, ordinary circle by Juan Diego - Monknow (@monknow) on CodePen.

我们已经知道了要使用的公式，所以可以定义一些方便的 CSS 变量：

:root {
  --circle-size: 60px;
  --amplitude: 200px; /* 振幅是距离，所以我们用像素单位 */
  --damping: 0.3;
  --frequency: 0.8;
  --offset: calc(pi/2); /* 这和 90deg 是一样的！(不过是用弧度表示) */
}

有了这些变量，我们可以使用像 GeoGebra 这样的工具来预览动画在图上的样子：

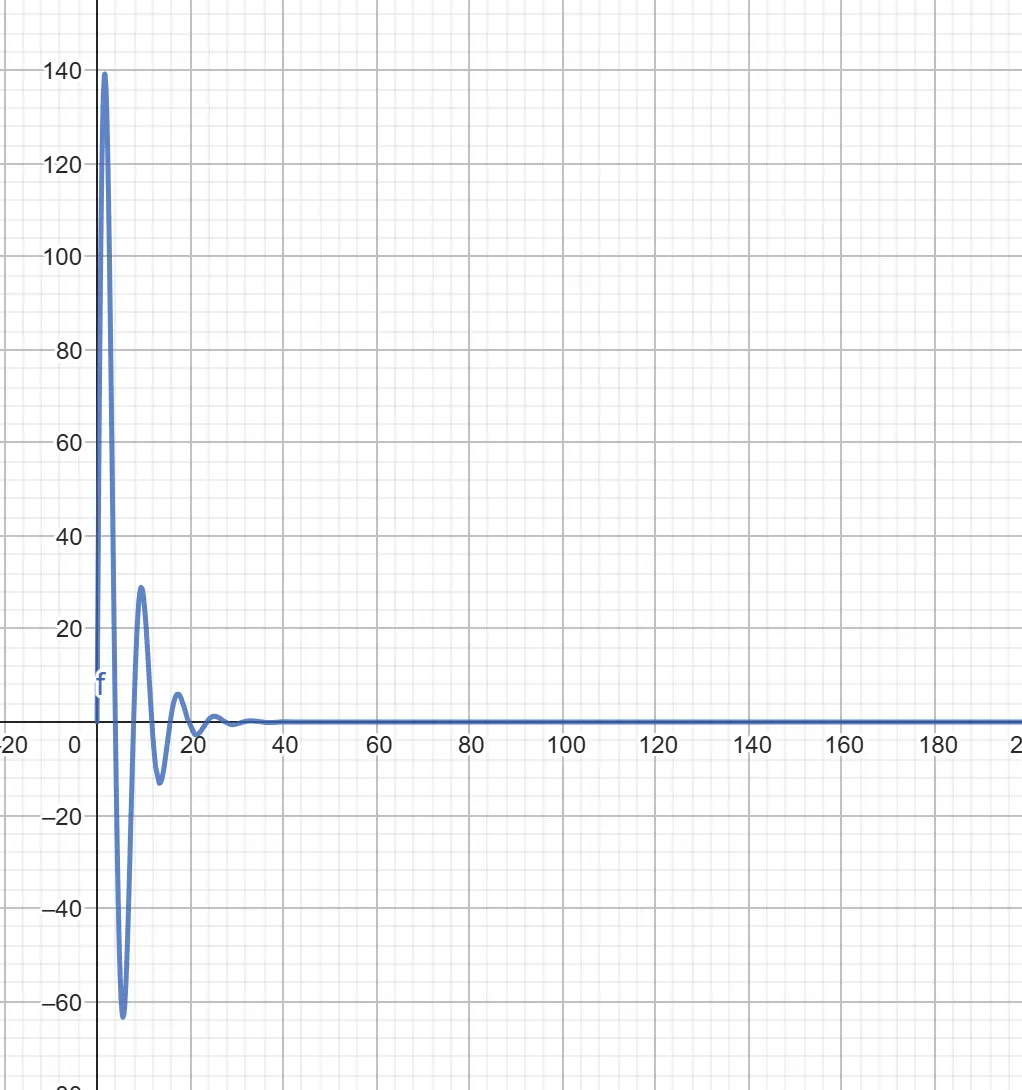
damped_graph_w17bzc

从图上我们可以看到，动画从 0px 开始（多亏了我们的偏移量），然后在 140px 左右达到峰值，并在大约 25s 时消失。我可不想等 25 秒才看到动画结束，所以我们来创建一个 --progress 属性，它将在 0 到 25 之间进行动画，并作为我们函数中的“时间”。

记住，要为自定义属性设置动画或过渡，我们必须使用 @property 规则来注册它。

@property --progress {
  syntax: "<number>";
  initial-value: 0;
  inherits: true;
}

@keyframes movement {
  from { --progress: 0; }
  to { --progress: 25; }
}

剩下的就是实现前面提到的元素运动公式了，用 CSS 的术语写出来是这样的：

.circle {
  --oscillation: calc(
    (exp(-1 * var(--damping) * var(--progress))) *
    var(--amplitude) *
    cos(var(--frequency) * (var(--progress)) - var(--offset))
  );
  transform: translateX(var(--oscillation));
  animation: movement 1s linear infinite;
}

See the Pen Example Damped Oscillation by Juan Diego - Monknow (@monknow) on CodePen.

这本身就提供了一个相当令人满意的动画，但阻尼运动只在 x 轴上。如果我们在两个轴上都应用阻尼运动会是什么样子呢？要做到这一点，我们可以为 x 轴复制相同的振荡公式，但将 cos() 替换为 sin()。

.circle {
  --oscillation-x: calc(
    (exp(-1 * var(--damping) * var(--progress))) *
    var(--amplitude) *
    cos(var(--frequency) * (var(--progress)) - var(--offset))
  );
  --oscillation-y: calc(
    (exp(-1 * var(--damping) * var(--progress))) *
    var(--amplitude) *
    sin(var(--frequency) * (var(--progress)) - var(--offset))
  );
  transform: translateX(var(--oscillation-x)) translateY(var(--oscillation-y));
  animation: movement 1s linear infinite;
}

See the Pen Example Damped Oscillation (Both axes) by Juan Diego - Monknow (@monknow) on CodePen.

这更令人满意了！一个环形的_并且_带有阻尼的运动，全靠 cos() 和 sin()。除了看起来很棒，这在实际布局中能怎么用呢？

我们不必费力去想。举个例子，看看我最近做的这个侧边栏，菜单项以阻尼运动的方式弹入视口：

See the Pen Damped Menu Bar by Juan Diego - Monknow (@monknow) on CodePen.

很酷，对吧？！

目录CONTENT

CSS “最令人讨厌”的特性：cos() 和 sin()

译者声明

CSS “最令人讨厌”的特性：cos() 和 sin()

CSS 三角函数：“最令人讨厌”的 CSS 特性

`cos()` 和 `sin()` 到底是什么？

环形布局

波浪形布局

阻尼振荡动画

评论区

CSS “最令人讨厌”的特性：cos() 和 sin()

译者声明

CSS “最令人讨厌”的特性：cos() 和 sin()

CSS 三角函数：“最令人讨厌”的 CSS 特性

cos() 和 sin() 到底是什么？

环形布局

波浪形布局

阻尼振荡动画

评论区

`cos()` 和 `sin()` 到底是什么？